Introduction
The goal of this was to be introduced to a variety of ways of correcting remotely sensed images for the effects of atmospheric interference. This was done in a variety of different methods. These methods are as follows 1) Empirical Line Calibration (ELC), 2) Dark Object Subtraction, and 3) Multidate Image Normalization. The images for this lab were provided by Cyril Wilson and were collected from Landsat 5 and Landsat povided by Cyril Wilson and were collected from Landsat 5 and Landsat 7.
Methods
Empirical Line Calibration
The first objective of this lab was to use Empirical Line Calibration (ELC) to clear up atmospheric interference for images of northwestern Wisconsin. To complete an ELC atmospheric correction this equation (fig 1). This equation takes the images separate bands, gain and offset. This equation was calculated using a built-in model in Erdas_Imagine by collecting GCPs. These GCPs were collected on series of different materials, these include asphalt roads, coniferous forests, grass, aluminum roofs, and a lake. The values collected from the GCPs were then compared to values in the USGS V4 and ASTER spectral libraries. Once the GCPs are collected and their spectral profiles compared to that of those in the spectral libraries, the
view-preprocessed-atmospheric adjustment tool was used to run regression equations between the results. Once this was completed, a new image was created that corrected for atmospheric interference.
 |
| Figure 1. Equation used for Empirical Line Calibration |
Dark Object Subtraction
The next atmospheric correction method used was Dark Object Subtraction. To complete this method, it needs to be completed in two steps. The first step is to convert satellite image to at-satellite spectral radiance. That is done by using the equation from figure 2. The inputs are collected from the images metadata. This equation needed to applied to each of the six bands for the image (fig. 3). To do this, a model was created in model maker (fig. 4). The model was run to create new radiance images (fig. 5).
 |
| Figure 2. Equation used to convert satellite image to at-satellite spectral radiance |
 |
| Figure 3. The at-satellite spectral radience conversion formula being applied to band 1 |
 |
| Figure 4. model created that incorporates the equations for the six different models |
 |
| Figure 5. Radiance images created using the model in Figure 4. |
After the model was run, the next step was to convert the newly-created at-satellite radiance images to true surface reflectance images (figure 5.). The inputs were collected from the original images meta data and the radiance image histograms (fig 6). To complete this another model was created to implement the new equation (fig. 7)
 |
| Figure 5. Equation used to convert at-satellite radiance to true surface reflectance. |
 |
| Figure 6. Histogram of band 1 of the Landsat TM image. The path radiance for the image is calculated from zero to the start of the histogram |
 |
| Figure 7. Model used to convert at-satellite radiance to true surface reflectance for each of the six reflective bands |
After the model was run six new images were created and stacked together creating a DOS image (fig. 8.)
 |
| Figure 8. Final DOS image after stacking the different bands together. |
Multidate Image Normalization
The next part of this lab was to create a atmospheric corrected image for Chicago using Multidate Image Normalization. This method uses two different images collected at different dates and compare their spectral reflective values using regression equations to create a new normalized image. To do this, GCPs are collected for the two images and their spectral signatures are recorded into spectral profiles (fig. 9).
 |
| Figure 9a. GCPs collected from various surfaces in the two images |
 |
| Figure 9b. The spectral signatures collected from the two images |
After spectral signatures were recorded they were then entered in to excel (fig. 10) where regression equations could be created for the each band between the two images after scatter plots were created (fig. 11)
 |
| Figure 10. The spectral signatures collected at the different GCPs for the six different reflective bands |
 |
| Figure 11. Scatter plots created for each of the bands for both the Chicago_2000 and Chicago_2009 images. |
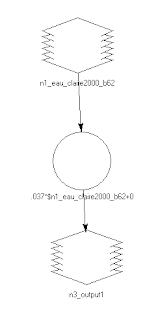
The equations from the scatter plots were entered into a model that created a new normalized each for each band. Once each bands image was created (fig. 12), they were then stacked to make one image that consisted of the different bands (fig. 13).
 |
| Figure 12. Normalized images of each of the reflective bands |
 |
| Figure 13. Layer stacked Multidate Normalized image. |
Results
ELC
Once the ELC image was created the new ELC image was compared to the original uncorrected image (fig. 14). To the naked-eye there are is not a large amount of change between the two images (fig. 14). The ELC corrected image is slightly sharper and is more vibrant in color. To examine the effectiveness of the ELC method, spectral signatures between the two images were taken. When looking at the spectral profile for healthy vegetation in the two images (fig. 15), it can seen that the ELC image has less atmospheric interference in the band 1 (blue band). This is because atmospheric scattering has been removed from the image. Similar trends can be seen when looking at the spectral profile of a local lake (fig. 16).
 |
| Figure 14. The two images side-by-side. The original image on the left and the corrected ELC image on the right. Between the two images only a slight difference between the images can be seen as the ELC image is slightly darker. |
 |
| Figure 15. Spectral signatures collected for healthy vegetation for the original (left) and ELC corrected image (right). |
 |
| Figure 16. Spectral signatures collected for lake Wissota in northwestern Wisconsin. The original image is on the left and the corrected image on the right. Decreases can be seen in band 1 in the corrected image as atmospheric interference has been removed. |
DOS
Much like the ELC image discuessed above, when viewing the original image and corrected image side-by-side (fig. 15) the differences between the images isn't very noticeable but more noticeable than the ELC image. Again, to spectral profiles of the two images were collected. Looking at simailar materials as in the ELC method, we can see similar results when looking at the spectral profiles. Looking at the spectal profiles a decrease in band 1 can be seen again as the effects of atmospheric interference has been removed from the image.
 |
| Figure 15. DOS image (right) and original image (left) side-by-side |
 |
| Figure 16. Spectral profile for healthy vegetation with the DOS image on the left and original image on the right. |
Multidate Image Normalization
As in the previously discussed atmospheric correction methods the images are shown side-by-side (fig. 17). When comparing the spectral profiles of the two images (fig. 18), a decrease in the reflective signature of band 1 can be seen in the normalized image.
 |
| Figure 17. Original image (left) and the corrected image (right) compared side-by-side. |
 |
| Figure 18. Spectral profiles of deciduous forest in the two images (normalized profile on the left and original on the right) |
Conclusions
This lab was successful in demonstrating the effectiveness of the different atmospheric correction methods. When using the ELC method, an important factor to consider is that values obtained from the spectral libraries may not be entirely accurate for the image that is being corrected. This is because the material in the image may not be the same material in the spectral library. This difference will lead to inaccuracies in the final product. Of the three methods discussed above, the most effective atmospheric correction method is the DOS method. This method requires the most information on the actual images to be accounted for.